决策树的简介
决策树是通过一系列规则对数据进行分类的过程。
在wiki中,它的定义如下:
决策论中 (如风险管理),决策树(Decision tree)由一个决策图和可能的结果(包括资源成本和风险)组成, 用来创建到达目标的规划。
机器学习中,决策树是一个预测模型,适用于监督学习,可解决回归和分类问题。它代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表某个可能的属性值,而每个叶节点则对应从根节点到该叶节点所经历的路径所表示的对象的值。
举例来说,决策树分类的思想类似于找对象。想象这样一个场景,一个女孩的母亲要给女儿介绍对象,于是就有了以下对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑:
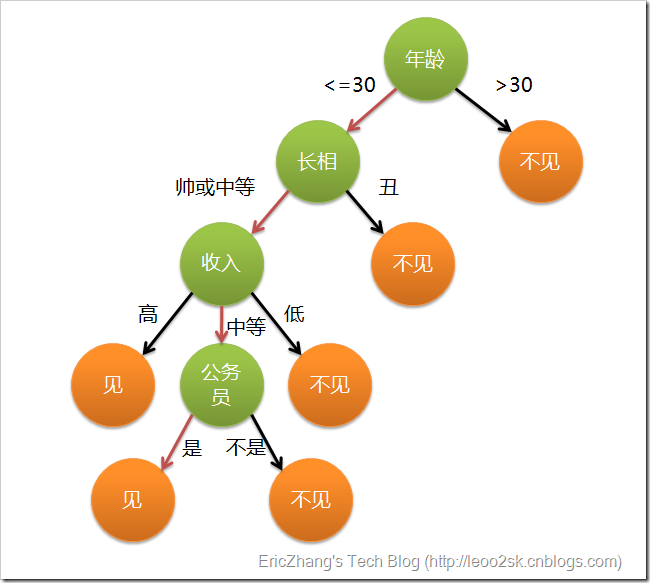
可以看到,决策树的决策过程非常直观,容易被人理解。目前决策树是应用最为广泛的归纳推理算法之一,在数据挖掘中受到研究者的广泛关注。
决策树的分类
在数据挖掘中,决策树主要有两种类型:
- 分类树 输出的结果是样本的类别,是离散值
- 回归树 输出的结果是一个实数,是连续值
常用的决策树算法有:
- ID3算法:Iterative Dichotomiser 3,由Ross Quinlan发明,以信息增益度量属性选择
- C4.5算法:原理类似ID3算法,不同的是属性选择使用的是信息增益率
- CART算法:Classification And Regression Tree,决策树的一种,以GINI指数作为度量数据,采用二分递归分割生成二叉树
ID3算法
ID3算法本质上是使用信息增益作为树分区划分的属性度量条件。 那么,什么是信息增益?
所谓信息增益就是指在系统中有无该属性时带来的信息量的变化。信息增益是属性选择中的一个重要指标,它定义为一个属性能够为分类系统带来多少信息,带来的信息越多,该属性就越重要。而信息量,就是熵。
熵定义为信息量的期望值。熵越大,一个变量的不确定性越大,它带来的信息量就越大。 计算信息熵的公式为:
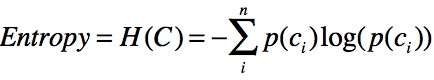
其中p为出现c分类时的概率。
那么如何计算一个属性的信息增益? 首先我们需要先根据信息熵公式计算出系统的平均熵值H(C),然后根据某个属性计算条件熵:
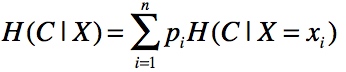
这是指属性X被固定时的条件熵。因为X可能的取值有n种,所以在计算条件熵时需要计算n个值,然后取均值(通过概率计算)。
最后通过将某分类的系统熵减去某个属性的条件熵,从而得到该属性的信息增益:
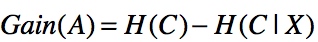
一个属性的信息增益越大,表明该属性对样本的熵减少能力越强,也就是说确定这个属性会使系统越稳定有序(熵越小系统越稳定),那么该分区的纯度也就越高。
一个示例
假设有一组数据:
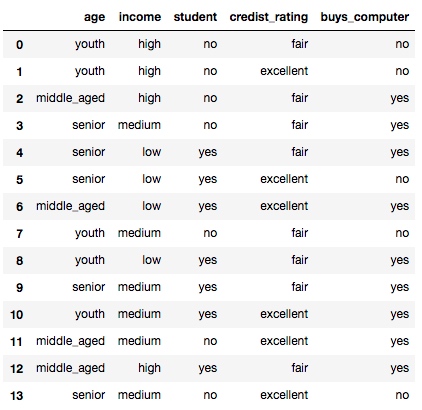
我们想要根据age、income、student、credist_rating推测buys_computer,首先我们需要计算buys_computer的系统平均熵:
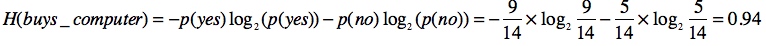
然后计算固定age属性时的条件熵:
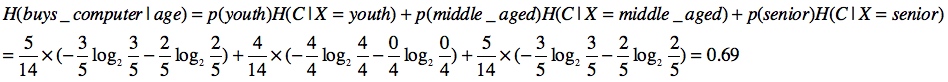
那么age的信息量增益等于:
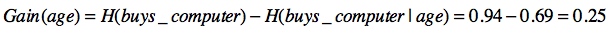
同理可计算出其他属性的条件熵:
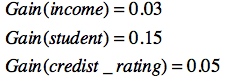
由于属性age具有最高的信息增益,那么就选择它作为分裂特征。然后递归这个过程,从而生成决策树。
Python实现
以下是我通过Python实现的ID3代码(仅作为示例,没有考虑任何优化),使用pandas和anytree包简化了实现过程:
import pandas as pd
from math import log
from anytree import Node, RenderTree
from anytree.dotexport import RenderTreeGraph
def create_decision_tree_id3(df, y_col):
# 计算H(C)
def h_value():
h = 0
for v in df.groupby(y_col).size().div(len(df)):
h += -v * log(v, 2)
return h
# 计算某一个属性的信息增益
def get_info_gain_byc(column, df, y_col):
# 计算p(column)
probs = df.groupby(column).size().div(len(df))
v = 0
for index1, v1 in probs.iteritems():
tmp_df = df[df[column] == index1]
tmp_probs = tmp_df.groupby(y_col).size().div(len(tmp_df))
tmp_v = 0
for v2 in tmp_probs:
# 计算H(C|X=xi)
tmp_v += -v2 * log(v2, 2)
# 计算H(y_col|column)
v += v1 * tmp_v
return v
# 获取拥有最大信息增益的属性
def get_max_info_gain(df, y_col):
d = {}
h = h_value()
for c in filter(lambda c: c != y_col, df.columns):
# 计算H(y_col) - H(y_col|column)
d[c] = h - get_info_gain_byc(c, df, y_col)
return max(d, key=d.get)
# 生成决策树
def train_decision_tree(node, df, y_col):
c = get_max_info_gain(df, y_col)
for v in pd.unique(df[c]):
gb = df[df[c] == v].groupby(y_col)
curr_node = Node('%s-%s' % (c, v), parent=node)
# 如果属性没有用完
if len(df.columns) > 2:
# 如果分区纯度是100%,则生成类别叶子节点
if len(gb) == 1:
Node(df[df[c] == v].groupby(c)[y_col].first().iloc[0], parent=curr_node)
else:
# 如果分区不纯则继续递归
train_decision_tree(curr_node, df[df[c] == v].drop(c, axis=1), y_col)
# 如果属性用完,则选择数量最多的类别实例作为类别叶子结点
else:
Node(df[df[c] == v].groupby(y_col).size().idxmax(), parent=curr_node)
root_node = Node('root')
train_decision_tree(root_node, df, y_col)
return root_node
df = pd.read_csv('~/allele.csv')
root_node = create_decision_tree_id3(df, 'buys_computer')
for pre, fill, node in RenderTree(root_node):
print("%s%s" % (pre, node.name))
RenderTreeGraph(root_node).to_picture("decision_tree_id3.png")

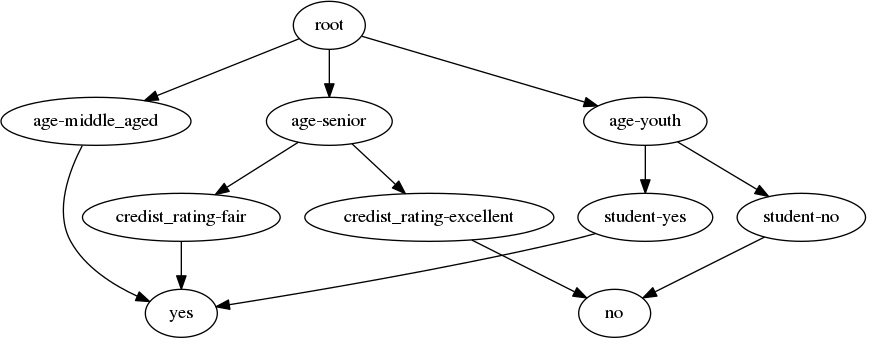
参考文献:
- http://hunch.net/~coms-4771/quinlan.pdf
- https://zh.wikipedia.org/wiki/%E5%86%B3%E7%AD%96%E6%A0%91%E5%AD%A6%E4%B9%A0
- http://www.cnblogs.com/wentingtu/archive/2012/03/24/2416235.html
- http://blog.csdn.net/dream_angel_z/article/details/45623107
- http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html
- http://anytree.readthedocs.io/en/latest/dotexport.html
(待续)